Zonal polynomial

In mathematics, a zonal polynomial is a multivariate symmetric homogeneous polynomial. The zonal polynomials form a basis of the space of symmetric polynomials.

They appear as zonal spherical functions of the Gelfand pairs 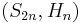$(S_{2n},H_n)$ (here, 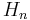$H_n$ is the hyperoctahedral group) and 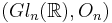$(Gl_n(\mathbb{R}), O_n)$ , which means that they describe canonical basis of the double class algebras $\mathbb{C}[H_n \backslash S_{2n} / H_n]$ and $\mathbb{C}[O_d(\mathbb{R})\backslash M_d(\mathbb{R})/O_d(\mathbb{R})]$ .

They are applied in multivariate statistics.

The zonal polynomials are the 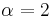$\alpha=2$ case of the C normalization of the Jack function.

References

Robb Muirhead, Aspects of Multivariate Statistical Theory, John Wiley & Sons, Inc., New York, 1984.